イベント出演いたします!太陽のマルシェ ナイトマルシェ@勝どき
ファゴットのS です。
まだ大暑まで半月ほどあるのに、今ままでにない暑さに参ってしまいますね。
暑さと湿度でへたるのは身体だけでなく、楽器も同じです。木管楽器には音高を変えるための沢山の穴(トーンホール)があって、それを指やタンポという、フェルトや厚紙を革などで巻いたもので押さえるのですが、このタンポが厄介で、夏場になるとベタついてしまいます。
特に私の楽器ですとトーンホールの表面にニスが塗ってあり、これにタンポの樹脂コーティングが貼り付いてペタペタと鳴ってしまいます、、、色々と工夫して使っているのですが、ヨーロッパの乾燥冷涼な気候に合わせて作られた楽器を日本で使う苦労を実感する季節です。
さて、これだけ暑い夏となれば暑気払いせずにはいられませんよね!?
もう頭の中でビールの泡が弾けているあなたにピッタリの、イベントと演奏のご案内です。
この度、「太陽のマルシェ」というイベントにて演奏させていただくことになりました!
通常は日中に開催しており、オーガニック食材などこだわりの食品を買ったり食べたり出来るのですが、今度の7月14日の会では夜も飲食をお楽しみいただけます。
その夜の部にサーガラのメンバーがお邪魔して演奏させていただきます。
プログラムも定期演奏会のレパートリーから一転、親しみやすい名曲を中心にアソート致しました。
サーガラの演奏を聞き(流し)ながら、素敵なディナーをお楽しみいただければと思います。一同お待ちしております。
太陽のマルシェ ナイトマルシェ
2018年7月14日(土)
18時〜21時(このうちに30分程度のプログラムを2回ほど演奏します)
@月島第二児童公園(都営地下鉄大江戸線『勝どき』駅下車、A4a出口、A4b出口すぐ)
※雨天・荒天中止
公式HP: http://timealive.jp/

次回演奏会情報! 第七回定期演奏会
こんにちは
サーガラ のホルンです
次回プログラムが決定しポスターデザインが出来上がりました!
ぜひ演奏会にお越しいただければと思います。
【次回演奏会情報】
サーガラ木管五重奏団
第七回定期演奏会
2018年10月27日(土)
16:30 開場 17:00 開演
@代官山教会
八重奏曲 / ヒンデミット
木管五重奏曲ハ短調 op. 91, no. 6 / ライヒャ
ポスター

ポスターについて
前回からマンデルブロ集合をPythonで描き始めたのですが、
今回もマンデルブロ集合を採用しました。
秋らしい色合いを意識してみました。
幾重にも連なる輪っかのような模様がとても印象的で、どこかで使いたいなあとずっとストックしていたものでした。
マンデルブロ集合は数列の発散具合を絵にしたものなので
なかなか色の調整が難しく、そこに一番時間がかかります。
本当は描いた絵のデータだけを残しておいて、色の調整だけ後からやれば良いのですが、ついついその場で計算してしまいがちです。
現代の計算技術に感謝しなくてはなりませんね。
さて、いよいよマンデルブロ集合もネタ切れ、、、、
次どうしようかなあ、、、、
なぜなぜ管楽器(その7):1次元波動方程式の導出 後編
こんにちは!
サーガラのホルンです。
今回はいよいよ波動方程式の導出です!
前回のおさらいですが、前回はポアソンの法則から

という式を導きました。
変数xは管内の位置、tは時刻を表します。
また、pは音圧、γは気体の比熱比、P0は大気圧、uは気体分子の変位(元ある位置からのずれ)を表します。
これを無理やり日本語にすると「ある地点での音圧pは、ある地点とちょっと先の地点での空気分子の位置のずれuの差に比例する」ということになります。
ものすっっっごく分かりずらいですが、まあそういうことです。
導出については前回の記事をご覧ください。
さて本題です。
今までは熱力学の観点から攻めてきましたが、
ここからは力学(古典力学)の観点から攻めてみましょう。
古典力学といえばみなさんおなじみのニュートンの運動方程式です。

高校物理学でもやりますね。
この運動方程式はアイザック・ニュートンの著書プリンキピアに載っている
運動の法則の2番目に書かれているものです。
運動の法則:第二法則
物体に力が働くとその力の方向に加速度が生じる。その加速度の大きさは力に比例し、物体の質量に反比例する。
なのでちゃんと考えると上式はまずく、まずベクトルで考えなければなりません。また、第二法則の内容をそのまま式で表すと

となります。
今考えているのは一次元で1方向しかないので、それを実数の正負で表すため、

で問題ないのです。多次元を扱う場合はしっかりとベクトルで扱う必要があります。
話が逸れてしまいましたが、ニュートンの運動方程式を今のモデルに当てはめてみたいと思います。前記事でのモデルを図に表すと下図のようになります。

断面積S厚さΔxの空気柱の塊を考えます。
するとこの空気の密度をρとして、質量は

と表すことができます。一方で加速度は空気中分子の加速度なので、
変位uを時刻で2回微分したものが加速度となります。

力は断面積x音圧なので以下のようになります。いつもの通り微分を使って近似します。

材料が揃いました。
これをma=Fに代入すると以下の式になります。

両辺SΔxで割れるので割ると

という式が得られます。
ここで、前回ポアソンの法則から得た式

をxで変微分して上式に代入すると

となります。
書き直すと

となります。
ここで、便宜的に右辺の係数をcの2乗と書くことにします。
すると運動方程式は以下のようになります。

これが求めたかった方程式の気柱の波動方程式です。
お疲れ様でした。
やっと空気中を伝播する音波の基礎方程式を導くことができました。
スタート地点に立ちました。
次回からはこの方程式の解き方について触れたいと思います。
なぜなぜ管楽器(その6):1次元波動方程式の導出 前編
こんばんは、
サーガラ のホルンです。
なんだかんだで
演奏会後は
更新頻度が落ちてしまいます。
すみません。
気を取り直して
今回はいよいよ波動方程式の導出です!
波動方程式というとなんだかとても難しく感じてしまいますが、
一言で表すと、
波の伝わり方を表した方程式
です。
この波動方程式は今回求めるものと実際の形は
異なるかもしれませんが、
周りにあふれています。
怖い地震

見えている光

聞こえてくる音
生活には欠かせない電線を伝わる電流

これらも波動方程式に従って空間を伝わっています。
なんだかとっても身近ですね
今回はまっすぐな管の中の波動方程式を求めます。
以前の記事
にて音波の性質を紹介しています。その中で
音波は疎密波と呼ばれる波で、空気中では空気中分子が
集まったり離れたりを繰り返して音波を伝えます。
イメージとしては下記youtubeの解説がわかりやすいと思います。
下のyoutubeの縦波が私の言いたい疎密波に相当します。
まさにこの疎密波のイメージで
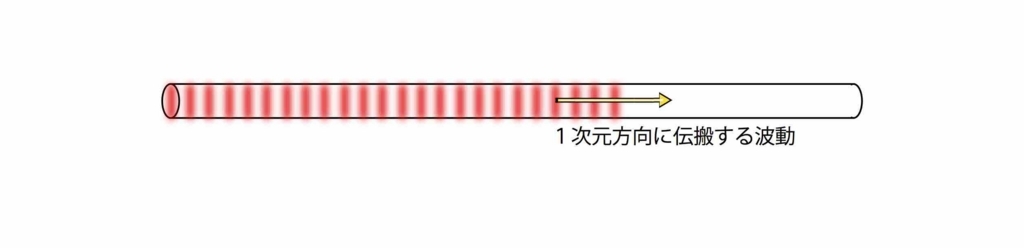
波動方程式を導出していくことにしましょう。
さて、前置きが長くなりましたが、
ここからいよいよ本題です。
まずは気体の性質について考えましょう。
音波振動による気体の振動は十分に速く熱のやり取りはないものとして考えます。
するとポアソンの法則が成立します。
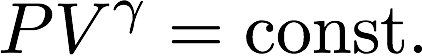
いきなり数式が出てきましたが、これは断熱条件下での気体の圧力と体積の関係を表したものです。Pは圧力、Vは体積を表します。
Vの右上についているものは定数でギリシャ文字のガンマです。
物理的には比熱比と呼ばれる量になっています。
ここも深く入ると面白いのですが今回は我慢、、、、
ガンマは気体の性質を表したただの数字だと思ってください。
右辺のconst.というのは一定という意味です。
ということは気体の体積を小さくすると圧力が大きくなり、
気体の体積を大きくすると圧力が下がるとこの法則は言っています。
その変化の仕方を数式にしたものだと考えてください。
さて、ここで音が無い時とある時の比較を行いたいと思います。
音がない時は気体中の粒子も振動していません。
この音がない状態である微小空間を取り出して考えます。
具体的には下図のVで示した領域です。
今はまっすぐな管を考えており、その断面積をSとします。
厚さをΔxとしてV=SΔxが微小領域です。
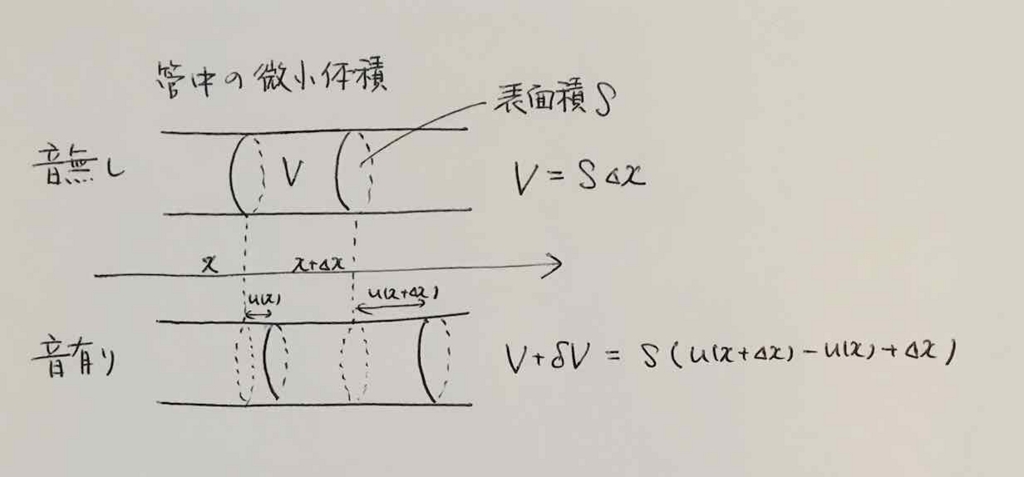
音が無い状態から音がある状態に変化させた時、空気中分子は振動します。
この時、元の微小空間にあった分子で構成される変化した微小空間との比較を行います。
ここでもポアソンの法則は成り立っているので、以下の式が成立します。
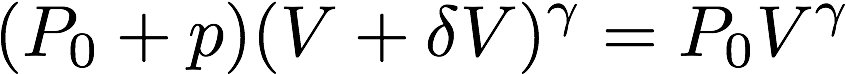
いきなり難しくなってきましたが、めげずに行きましょう。
P0は大気圧、pは音によって変化した圧力で音圧と呼ばれます。
δVはデルタVと読み、元の微小空間からの体積変化を表します。
体積、圧力が変化してもそれらの圧力と体積のガンマ乗の積は一定の値をとるので、上式が成立します。
ここで、左辺を展開してみましょう。
以前の記事の微分の知識を応用すると
音による体積変化量はとても小さいので

という式が成り立ちます。
真ん中のニョロん(〜)というのは近似しますよという意味で
だいたい同じです!ということを言っています。
上式を使って左辺を計算すると
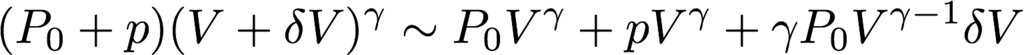
となります。ここで音圧とデルタVの積はとても小さい量なので無視しています。
もうちょっと難しい言い方をすると、近似では微小量の2次以上の項を無視しています。
従って、元の式から
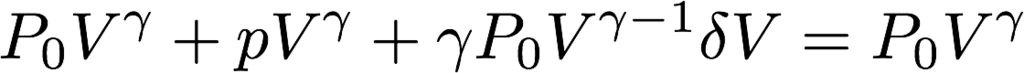
のように変形されました。
さらに式変形を進めると
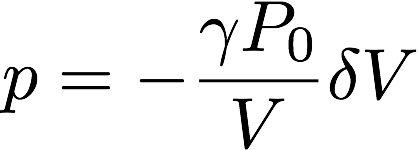
このような関係式が得られます。
音圧と音による体積変化がだいたい比例の関係にあることがわかりました。
だいたいというのは先ほど近似を行っているためです。
この結果を信じて先に進むことにしましょう。
(余談)===============================================
物理学では数式をそのまま解こうとしても解けない問題がほとんどです。
そこで先人たちは偉大な手法を考え出しました。
それが近似という手法です。
これはもはや物理学の常套手段でより現実に近ければ近いことを解明しようとするほど良く用いる手法です。
そして、近似という手法は驚くべき成功を数々挙げてきました。
もはや近似なくして語ることができないことは山ほどあります。
身近な例では地上で働く重力が
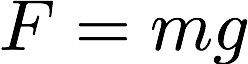
と表されることも万有引力の法則
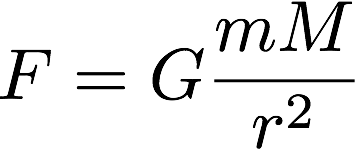
からゴニョゴニョ地球の形で積分したり積分したり積分したりすると求めることができます。
===============================================
次に
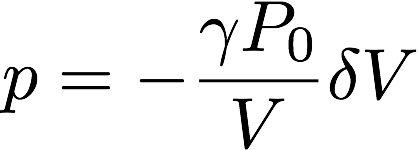
のδVについて考えてみましょう。
ここで変位というものを導入します。
ある位置の空気中粒子は音によって振動します。
その振動でのズレ具合を表したものです。
例えば下図位置xでの音による粒子のズレ、すなわち変位は

で表されます。

本当は時刻の関数でもあるので時刻をtとして
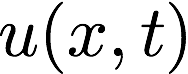
と書くべきですが、今は時刻については考慮しないので、無視します。
あとでちゃんと書き下す時に復活させます。
さて、上図にて音ありの場合の変化した微小領域V+δVを計算します。
右方向を正に取ります。
位置xの変位がu(x)なので当然位置x+Δxでの変位はu(x+Δx)となります。
これらの情報からV+δVは

ここで
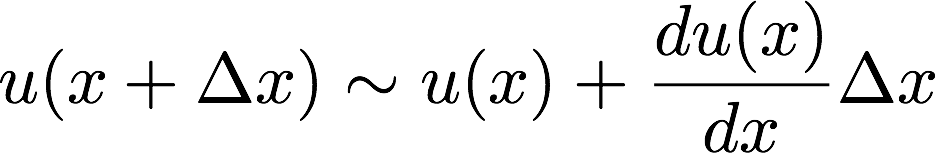
を用いました。詳しくは過去記事をご覧ください。
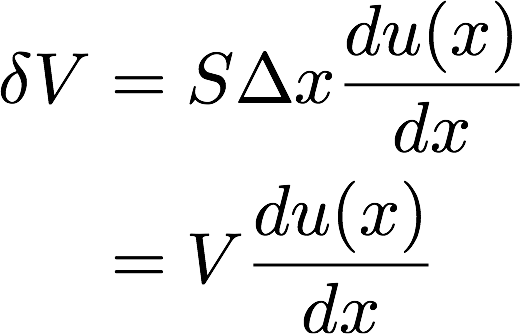
という関係が求まります。
先ほど求めた
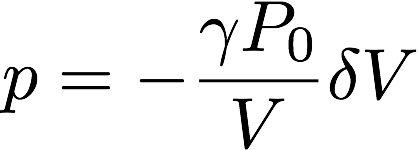
に代入すれば
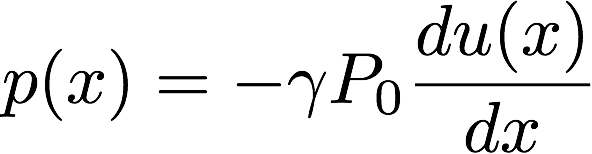
が求まります。ここで、実際は音圧も変位も時刻に依存するので、

微分の記号が変わりましたが、これは偏微分といい、今の場合時刻tを定数と思ってxについてだけ微分しなさいという意味です。
詳しくは過去記事を参照ください。
過去記事もそんなに詳しくないけど、、、、
ふう、、、
読んでいただいている方も
頭パンクしそうになると思うので
とりあえず今回はここまでにしましょうか
次回はいよいよ1次元波動方程式を導きます。
種明かしをすると
圧力と変位の関係式を代入することで求めることができます。
出発は

この図になります。
やっとここまできたー
長かった、、、、
おやすみなさい